SociologyBest

F(x)=G(lnx)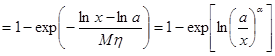

где a=1/Mh, а m=lna. Окончательно имеем функцию распределения F(x)=1 – (a/x)a доходов x³a, которая представляет собой распределение Парето.

Замечание 3.

Если учесть, что доходность акций и банковских депозитов может быть не только положительной, но и отрицательной, например, из-за инфляции, то можно использовать замечание 2 к примеру 1б для получения распределения доходов по функции распределения доходности, как только что было сделано. В этом случае получится хорошо известное логнормальное распределение дохода, которое используется во многих исследованиях.

Во всех последующих примерах будут использоваться как стандартные параметры так и параметры, включающие минимальный (a) и средний доходы (W).

Пример 1. Распределение Парето. Пусть распределение доходов w>0 имеет вид F(w)=[1 – (a/w)a]+, где [u]+ обозначает max (u, 0), а a – минимальный доход. В этом случае для существования математического ожидания W=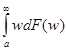=a необходимо, чтобы a>1, так как W>a и a=. Тогда ордината кривой Лоренца y=L(w) имеет вид L (w [1 – (a/w)=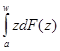=)a-1]+, а площадь l под кривой Лоренца l=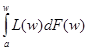=. Отсюда коэффициент Джини G=1–2l==. Очевидно, что при a>1 G>0 и G®0 при a®¥, а при a®1 G®1.

Пример 2. Равномерное распределение. Пусть распределение доходов равномерно на отрезке [a, b], т.е. F(w)=0 при w<a, F(w)=(w-a)/(b-a) при a£w<b и F(w)=1 при w³b. Известно, что среднее значение доходов W в этом случае равно (b+a)/2. Кривая Лоренца получается из соотношения L(w)=zF(z) dz=dz=(w2-a2)/(b2-a2). Площадь под кривой Лоренца l=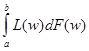=+, а коэффициент Джини G=1–2l. Удобно, как и ранее, выразить коэффициент Джини через средние доходы W и минимальные a. Так как W=, то коэффициент G=. Последнее означает, что равномерное распределение доходов дает G=0 при W=a и G=1/3 при W®¥.

Пример 3. Двухточечное распределение. Рассмотрим простейший случай, когда люди имеют доходы только двух размеров – минимальные a и максимальные b. В этом случае функция распределения F(w)=0, при w<a, F(w)=p, при a£w<b, и F(w)=1, при w³b, а математическое ожидание дохода равно W=pa+(1‑p) b. Теперь кривая Лоренца состоит из двух отрезков прямых линий, проходящих через точки (0,0), (p, p) и (1,1). Площадь треугольника между диагональю квадрата и сторонами, составляющими кривую Лоренца, будет равна 1/2‑l=0,5 (p-p), т.е. половине абсолютной величины определителя

Организация статистической отчетности в Российской Федерации
В настоящее время в соответствии с Положением о Федеральной службе государственной статистики, утвержденным постановлением Правительства РФ от 30 июля 2004г., главным учетно-статистическим центром в стране является Федеральная служба госу ...

Программа государственных гарантий оказания гражданам Российской Федерации бесплатной медицинской помощи.
В целях обеспечения конституционных прав граждан на получение бесплатной медицинской помощи Правительство РФ приняло постановление от 11.09.1998 N 1096 "Об утверждении государственных гарантий оказания гражданам Российской Федерации ...

Общественное сознание и типы обществ
В обществах традиционных искусство, религия и мораль первоначально существуют в слабо дифференцированном единстве. Наука очень тесно связана с донаучными формами познания (астрология, алхимия, различные виды магии и пр.), а право в основн ...