ЗаключениеСтраница 1
Теперь, когда рассмотрены несколько мер расслоения, в том числе дисперсия, отношение квартилей (децилей), энтропия, коэффициенты вариации и Джини можно их сравнивать между собой. Для этого воспользуемся тремя типами распределений среднедушевых доходов, которые уже также были приведены – это распределения Парето, равномерное и двухточечное.
Для такого сравнения, в качестве примера, примем, что минимальный среднедушевой доход a будет считаться единичным. В этом случае математическое ожидание доходов W будет равно k (или ka=W).
В этом случае функции распределения всех трех типов представимы в виде:
1) Парето – 1-
, при х>1 и 0 при х£1;
2) равномерное – 0 при х£1; 
, при 1<x£2k‑1 и
3) двухточечное – 0 при x£1, p при 1<x£
и 1 при x>.
Легко проверить, что математические ожидания всех трех типов распределения равны k (см. задачу 3).
Таблица 1. Меры расслоения
|
Распределения |
Дисперсия |
Энтропия |
Коэф. вариации |
Коэф. Джини |
|
Парето |
|
|
|
|
|
равномерное. |
|
|
|
|
|
двухточечное |
|
-p lnp- – (1‑p) ln (1‑p) |
|
|
Для получения функции Лоренца необходимо получить интеграл L(w)=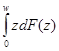
, который равен для распределения Парето (тип 1):
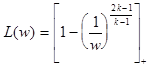, где [x]+=max [0, x]; для равномерного распределения (тип 2) L(w)=0 при w£1, L(w)=
при 1<w£2k-L(w)=1 при w>2k‑1, наконец, для двухточечного распределения (тип 3) имеем координаты кривой (ломаной) Лоренца (w, L(w)): L(w)=1/k. при 0<w£p,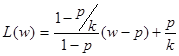 
при p<w£1, где w – доля людей, получающая долю доходов L(w).
Таким образом, кривая Лоренца (в данном случае, ломаная линия), состоит из двух отрезков прямых, соединяющих точки (0,0), (p, p/k) и (1,1), а площадь треугольника с вершинами в этих точках (см. задачу 4) равна 
.
Используемый ранее в главе интеграл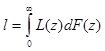 
будет встречаться далее, но в другом смысле и для других целей. Сейчас же обратим внимание только на то, что как L(w), так и F(w) – вероятностные меры. Поэтому величина l формально это уже написанный функционал от двух мер, притом необязательно L(w) связана с F(w), так как было отмечено ранее в этой главе.
Объект и предмет социологии
Основные компоненты знания. В социологии, как и в любой другой науке, имеются следующие основные компоненты: знание и средства его получения. Первый компонент — социологическое знание — включает в себя знание о знании (методологическое ...
«Холодные» и «горячие» конфликты в поведенческой модели У. Марстона
Среди психологов, изучавших поведение людей в конфликтных ситуациях, можно назвать Л.Козера (концепция позитивно-функционального конфликта), Р.Дарендорфа (конфликтная модель общества), К.Боулдинга (общая теория конфликта), К.Томаса (опрос ...
Роль идеологии в общественной жизни
Впервые термин идеология ввел в обиход французский философ и экономист А. Л. К. Дестют де Траси в 1801 г. в своем произведении «Элементы идеологии» для анализа ощущений и идей[1].
В этот период идеология выступает своеобразным философски ...